Simple Proof By Induction

Induction is really important so the best thing to understand induction is to do it yourself. We will prove the statement by induction on all rooted binary trees of depth d.

Mathematical Induction Proof By Induction Examples Steps

It is done by proving that the first statement in the infinite sequence of statements is true and then proving that if any one statement in.

Simple proof by induction. With simple induction you use if pkis true then pk1is true while in strong induction you use if piis true for all iless than or equal to kthen pk1is true where pkis some statement depending on the positive integer k. Few values of n and if you wish construct a standard proof by induction that it works. Thus 1 holds for n k 1 and the proof of the induction step is complete.

Construct squares composed of 1 6 and 8 squares. Mathematical induction is a proof technique not unlike direct proof or proof by contradiction or combinatorial proof. For our base case we need to show P0 is.

P0 and from this the induction step implies P1. All you do is adapt the proof strategy so that the basis is n0. For the base case we have d 0 in which case we have a tree with just the root node.

From that the induction step then implies P2 then P3 and so on. Many mathematical statements can be proved by simply explaining what they mean. Proof by mathematical induction.

Inductive proofs are similar to direct proofs in which every step must be justified but they utilize a special three step. 123n1n Xn i1 i. Xn i1 i2 Xn i1 Xi j1 2j 1 Xn i1 ni12i1 The last equality holds because each term of the form 2i 1 appears exactly n i 1 times in the double sum.

They are NOT identical but they are equivalent. Before we get to the induction proof you need to understand how an inductively defined set works. 1 per month helps.

By the principle of induction 1 is true for all n 2Z. Induction also works if you want to prove a statement for all n starting at some point n0 0. Thanks to all of you who support me on Patreon.

A proof by mathematical induction is a powerful method that is used to prove that a conjecture theory proposition speculation belief statement formula etc is true for all cases. It is a common mistake to check a few numbers and assume that the pattern holds for all others. We will prove by.

To appreciate the power of induction I will prove this by simply relying on our first two results namely Xn i1 i nn1 2 Xn i1 2i1 n2 The proof will require manipulations of sums. Your next job is to prove mathematically that the tested property P is true for any element in the set -- well call that random element k-- no matter where it appears in the set of elements. The symbol P denotes a sum over its argument for each natural.

Sn nn1n2n3 4. Proof by induction involves statements which depend on the natural numbers n 123. Then show by induction that if you can construct a square composed of n squares then you can construct a square composed of n 3 squares simply by cutting one of the squares into 4 more.

Proof by Induction - Examp. In this case we have 1 nodes which is at most 2 0 1 1 1 as desired. We write the sum of the natural numbers up to a value n as.

Instead of your neighbors on either side you will go to someone down the block randomly and see if they too love puppies. Well start by considering what induction means leaving mathematics aside. 3 In other words induction is a style of argument we use to convince ourselves and others that a mathematical statement is always true.

Mathematical Induction is a special way of proving things. As in other proof methods one should alert the reader at the beginning of the proof that this method is being used. Find and prove by induction a formula for P n i1 2i 1 ie the sum of the rst n odd numbers where n 2Z.

Let Pn be the sum of the first n positive natural numbers is nn 1 2 We show that Pn is true for all natural numbers n. The sum of the first n positive natural numbers is nn 12. RHS n 1 n 1 1 n 1 2 3 n 1 n 2 n 3 3.

What Is Proof By Induction. It often uses summation notation which we now briefly review before discussing induction itself. Of course a few examples never hurt.

By the Principle of Mathematical Induction we are done once we show. Each Pn follows from the previous like a long of dominoes toppling over. Show it is true for the first one.

1 P n 0 holds for small non-negative integers n 0 eg n 0 0 n 0 1 or n 0 2 and. You da real mvps. Show that if any one is true then the next one is true.

Then all are true. If youre really ambitious you can even show that the technique above summing the coefficients in the left diagonal by various factors of n k works using induction. Our First Proof By Induction Theorem.

Just because a conjecture is true for many examples does not mean it will be for all cases. Mathematical Induction is used to prove many things like the Binomial Theorem and equa-tions such as 1 2 n nn 1 2. Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true for all natural numbers positive integers.

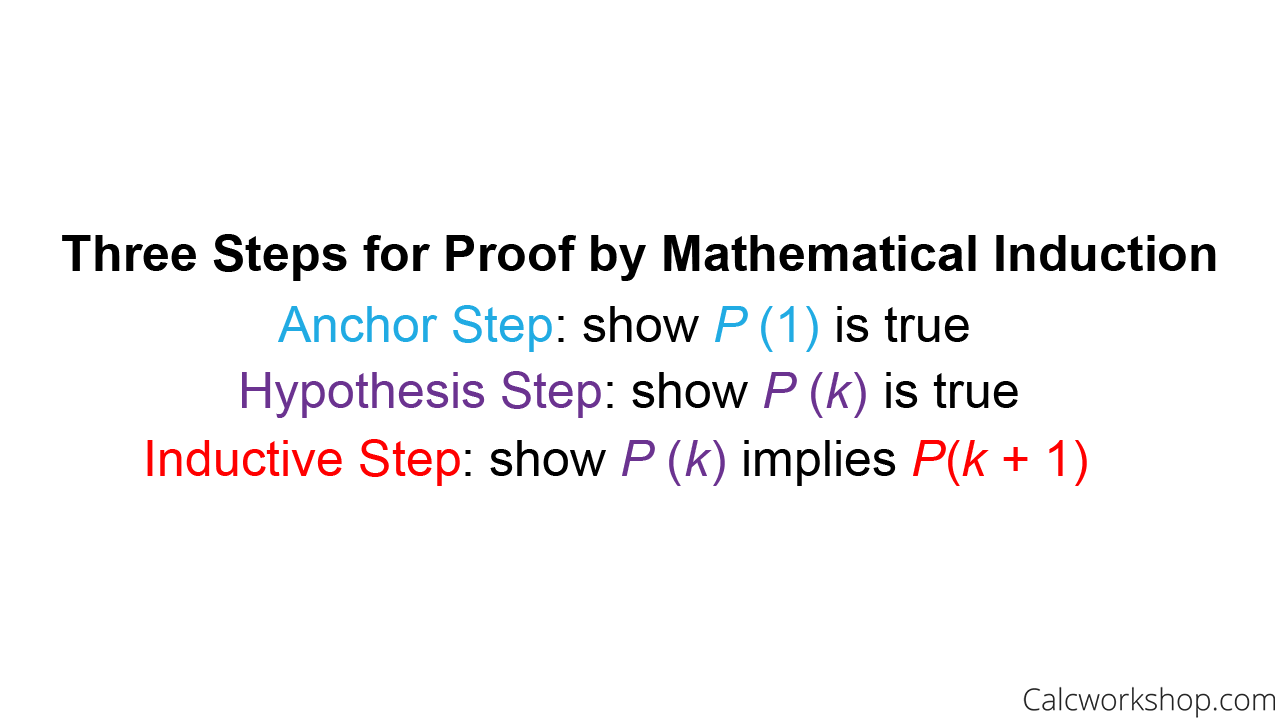
This is the induction step. It has only 2 steps.

Simple Factoring In Proof By Induction Mathematics Stack Exchange

Proof By Induction W 9 Step By Step Examples

Proof By Induction

Proof By Induction Sums 1 Fp1 Edexcel A Level Maths Youtube

Proof Writing How To Write A Clear Induction Proof Mathematics Stack Exchange

Induction Proof For A Summation Identity Youtube

Prove Using Induction N 2 7n 12 Geq 0 Where N Geq 3 Mathematics Stack Exchange

Mathematical Induction Tutorial

Proof By Induction W 9 Step By Step Examples

Mathematical Induction Tutorial

Proof By Induction There Are Different Ways To

Mathematical Induction Proof For The Sum Of Squares Youtube

Proof By Induction How Can I Get Familiar With It Mathematics Stack Exchange

Mathematical Induction Topics In Precalculus

Proof By Induction

2

Proof By Induction Advanced Higher Maths

Principle Of Mathematical Induction 5 Amazing Examples

Mathematical Induction Proofs Mathematics Stack Exchange